La medida de un verso
Para conocer la medida de un verso, debemos contar el número de sílabas.
Por ejemplo, el verso "luna lunera" tiene 5 sílabas.
Pero, además, hemos de tener en cuenta de qué tipo es la última palabra del verso
según la posición del acento.
- Si la última palabra del verso es aguda, se cuenta una sílaba más.
Por ejemplo: los brazos del calamar: 7 + 1 = 8 sílabas.
- Si la última palabra del verso es esdrújula, se cuenta una sílaba menos.
Por ejemplo: alcanzaron el séquito : 8 – 1 = 7 sílabas.
- Además, a veces para medir un verso hay que tener en cuenta la sinalefa.
La sinalefa se produce cuando una palabra de un verso acaba en vocal y la siguiente es una y o comienza por vocal o por h.
En ese caso las dos vocales se pronuncian juntas y se cuenta una sola sílaba y no dos. Por ejemplo: se hace camino al andar, 9 - 2 sinalefas + 1 aguda = 8 sílabas.
Según su medida, los versos pueden ser de dos tipos:
- Versos de arte menor son los que tienen 8 sílabas o menos.
- Los versos de arte mayor son los que tienen 9 o más.
La rima
La rima puede ser asonante o consonante:
- La rima asonante se produce cuando dos palabras tienen las mismas vocales
pero distintas consonantes a partir de la vocal tónica.
Por ejemplo: reja y oveja.
- La rima consonante se produce cuando dos palabras tienen las mismas
vocales y las mismas consonantes a partir de la vocal tónica.
Por ejemplo:directo y perfecto.
FICHA PARA DESCARGAR
ANALIZAR UN POEMA
Mostrando entradas con la etiqueta medida. Mostrar todas las entradas
Mostrando entradas con la etiqueta medida. Mostrar todas las entradas
martes, 31 de enero de 2017
martes, 24 de mayo de 2016
Medida de la superficie
MEDIR SUPERFICIES
El área de una figura plana es la medida de su superficie.
Calcular el área es contar el número de unidades cuadradas que ocupa.
UNIDADES DE SUPERFICIE DEL SISTEMA MÉTRICO DECIMAL
La unidda fundamental de superficie es el metro cuadrado m2.
Un metro cuadrado es la superficie que ocupa un cuadrado de un metro de lado.
Múltiplos del m2: km2 - hm2- dam2.
Submúltiplos del m2: dm1 - cm2 - mm2.
Estas unidades van de 100 en 100: 1m2 = 100 dm2 = 10.000 cm2 = 1.000.000 mm2.
ÁREA DE LOS PARALELOGRAMOS
El área del cuadro se calcula multiplicando lado por lado:
A = l x l
El área de un cuadrado de 3 cm de lado sería:
A = l x l = 3 cm x 3 cm = 9 cm2
El área del rectángulo y del romboide se calcula multiplicando la base por la altura.
A = b x a
El área de rectángulo de 4 cm de base y 2 cm de altura sería:
A = b x a = 4 x 2 = 8 cm2.
El área del rombo se calcula multiplicando la diagonal mayor por la diagonal menor y dividiéndolo por 2:
A = ( D x d ) : 2
El área de un rombo de 3 y 6 cm de diagonales sería:
A = ( 6 x 3 ) : 2 = 18 : 2 = 9 cm2.
ÁREA DE LOS TRIÁNGULOS
El área de un triángulo es la mitad del rectágulo:
A = ( b x a ) : 2
El área de un triángulo de 4 cm de base y 5 cm de altura sería:
A = ( b x a ) : 2 = ( 4 x 5 ) : 2 = 20 : 2 = 10 cm2
ACTIVIDADES INTERACTIVAS
LA SUPERFICIE
PERÍMETROS Y ÁREAS
CALCULAR PERÍMETROS Y ÁREAS
UNIDADES DE SUPERFICIE - AGREGA2
EJERCICIO CON UNIDADES DE SUPERFICIE
EJERCICIO DE ÁREA DE FIGURAS PLANAS
ÁREA DEL RECTÁNGULO Y EL TRIÁNGULO - GENMAGIC
CADA PUESTO EN SU ÁREA
FICHAS PARA DESCARGAR
FICHA REPASO 1
FICHA REPASO 2
FICHA AMPLIACIÓN 1
FICHA AMPLIACIÓN 2
El área de una figura plana es la medida de su superficie.
Calcular el área es contar el número de unidades cuadradas que ocupa.
UNIDADES DE SUPERFICIE DEL SISTEMA MÉTRICO DECIMAL
La unidda fundamental de superficie es el metro cuadrado m2.
Un metro cuadrado es la superficie que ocupa un cuadrado de un metro de lado.
Múltiplos del m2: km2 - hm2- dam2.
Submúltiplos del m2: dm1 - cm2 - mm2.
Estas unidades van de 100 en 100: 1m2 = 100 dm2 = 10.000 cm2 = 1.000.000 mm2.
ÁREA DE LOS PARALELOGRAMOS
El área del cuadro se calcula multiplicando lado por lado:
A = l x l
El área de un cuadrado de 3 cm de lado sería:
A = l x l = 3 cm x 3 cm = 9 cm2
El área del rectángulo y del romboide se calcula multiplicando la base por la altura.
A = b x a
El área de rectángulo de 4 cm de base y 2 cm de altura sería:
A = b x a = 4 x 2 = 8 cm2.
El área del rombo se calcula multiplicando la diagonal mayor por la diagonal menor y dividiéndolo por 2:
A = ( D x d ) : 2
El área de un rombo de 3 y 6 cm de diagonales sería:
A = ( 6 x 3 ) : 2 = 18 : 2 = 9 cm2.
ÁREA DE LOS TRIÁNGULOS
El área de un triángulo es la mitad del rectágulo:
A = ( b x a ) : 2
El área de un triángulo de 4 cm de base y 5 cm de altura sería:
A = ( b x a ) : 2 = ( 4 x 5 ) : 2 = 20 : 2 = 10 cm2
ACTIVIDADES INTERACTIVAS
LA SUPERFICIE
PERÍMETROS Y ÁREAS
CALCULAR PERÍMETROS Y ÁREAS
UNIDADES DE SUPERFICIE - AGREGA2
EJERCICIO CON UNIDADES DE SUPERFICIE
EJERCICIO DE ÁREA DE FIGURAS PLANAS
ÁREA DEL RECTÁNGULO Y EL TRIÁNGULO - GENMAGIC
CADA PUESTO EN SU ÁREA
FICHAS PARA DESCARGAR
FICHA REPASO 1
FICHA REPASO 2
FICHA AMPLIACIÓN 1
FICHA AMPLIACIÓN 2
viernes, 29 de abril de 2016
La medida de los versos
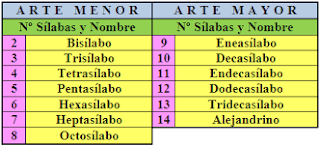
Los versos reciben distintos nombres según el número de sílabas que tienen.
Atendiendo a su medida, estas son las principales clases de versos:
- Bisílabos: 2 sílabas.
- Trisílabos: 3 sílabas.
- Tetrasílabos: 4 sílabas.
- Pentasílabos: 5 sílabas.
- Heptasílabos: 7 sílabas.
- Decasílabos: 10 sílabas.
- Alejandrinos: 14 sílabas.
A efectos métricos, no existen versos de una sola sílaba, porque si el verso está formado por una palabra monosílaba, esa palabra se considera aguda y se cuenta una sílaba más. Los versos más utilizados en poesía son los de ocho sílabas (octosílabos) y los de once (endecasílabos).
Versos de arte menor y de arte mayor
Hay dos grandes grupos de versos según su medida:
- Versos de arte menor los que tienen ocho sílabas o menos.
Por ejemplo:
En el soto ▶ 4 sílabas (tetrasílabo)
los alamillos bailan ▶ 7 sílabas (heptasílabo)
uno con otro. ▶ 5 sílabas (pentasílabo)
- Versos de arte mayor los que tienen más de ocho sílabas.
Por ejemplo:
Y vi que en vez de rosas y claveles ▶ 11 sílabas (endecasílabo)
ella tronchaba lirios con sus manos. ▶ 11 sílabas (endecasílabo)
ACTIVIDADES INTERACTIVAS
(Ejemplo en la página 24, actividades a partir de la página 25)
Atendiendo a su medida, estas son las principales clases de versos:
- Bisílabos: 2 sílabas.
- Trisílabos: 3 sílabas.
- Tetrasílabos: 4 sílabas.
- Pentasílabos: 5 sílabas.
- Heptasílabos: 7 sílabas.
- Decasílabos: 10 sílabas.
- Alejandrinos: 14 sílabas.
A efectos métricos, no existen versos de una sola sílaba, porque si el verso está formado por una palabra monosílaba, esa palabra se considera aguda y se cuenta una sílaba más. Los versos más utilizados en poesía son los de ocho sílabas (octosílabos) y los de once (endecasílabos).
Versos de arte menor y de arte mayor
Hay dos grandes grupos de versos según su medida:
- Versos de arte menor los que tienen ocho sílabas o menos.
Por ejemplo:
En el soto ▶ 4 sílabas (tetrasílabo)
los alamillos bailan ▶ 7 sílabas (heptasílabo)
uno con otro. ▶ 5 sílabas (pentasílabo)
- Versos de arte mayor los que tienen más de ocho sílabas.
Por ejemplo:
Y vi que en vez de rosas y claveles ▶ 11 sílabas (endecasílabo)
ella tronchaba lirios con sus manos. ▶ 11 sílabas (endecasílabo)
ACTIVIDADES INTERACTIVAS
(Ejemplo en la página 24, actividades a partir de la página 25)
FICHA PARA DESCARGAR
viernes, 4 de marzo de 2016
El verso y su medida
Los versos de los poemas tienen
diferente extensión.
Hay versos formados por una sola
palabra y versos que contienen muchas palabras.
La medida de los versos es uno de los
elementos que contribuyen a dar sonoridad a los poemas.
Generalmente, la medida o extensión de
un verso equivale a su número de sílabas.
Por ejemplo:
La - se - ño - ri - ta ▶
5 sílabas
del - a - ba - ni - co ▶
5 sílabas
va - por - el - puen - te ▶ 5
sílabas
del - fres - co - rí - o. ▶
5 sílabas
(Federico garcía Lorca)
A veces, todos los versos de un poema
tienen el mismo número de sílabas, pero otras veces se combinan en
un poema versos de distinta medida.
Reglas para medir versos
Para conocer la medida de un verso,
debemos contar su número de sílabas, pero además debemos tener en
cuenta estas reglas:
● Si la última palabra del verso es
aguda, se cuenta una sílaba más.
Por ejemplo:
La - más - be - lla - ni - ña ▶
6 sílabas
de - nues - tro - lu - gar ▶
5 sílabas + 1 = 5 ▶ 6 sílabas
● Si la última palabra del verso es
esdrújula, se cuenta una sílaba
menos. Por ejemplo:
Ai - re - de - mú - si - ca ▶ 6
sílabas - 1 = 5 ▶ 5 sílabas
La sinalefa es un fenómeno que se
produce cuando una palabra termina en vocal y la siguiente empieza
también por vocal o por h, o es una y.
En estos casos, las dos vocales se
pronuncian juntas y se cuentan como una sola sílaba. Por ejemplo:
Tres - mo - ri - llas - me e -
na - mo - ran ▶ 8 sílabas (sinalefa me-e)
RESUMEN
La medida de un verso equivale a su
número de sílabas.
Al medir versos, se cuenta una sílaba
más si la última palabra es aguda y una sílaba menos si la última
palabra es esdrújula.
La sinalefa se produce cuando dos
sílabas contiguas se cuentan como una sola.
REGLAS PARA MEDIR VERSOS
El acento en la última palabra del
verso:
Regla 1: Última palabra aguda: cuando
el verso acaba en palabra aguda, o en un monosílabo, se cuenta una
sílaba más.
El – rí – o – Gua –dal – qui
– vir ...................(7 + 1 = 8 sílabas)
... ¿Adónde el camino irá? ........................(7 + 1 =
8)
Yo voy cantando, viajero ..........................(8)
A lo largo del sendero ............................ (8)
- La tarde cayendo está. .........................(7 + 1
= 8 )
Regla 2: Si es llana no varía el
número de sílabas
A – lo – lar – go – del - sen
– de - ro ........................ (8)
Regla 3: Última palabra esdrújula:
cuando el verso acaba en palabra esdrújula, se cuenta una sílaba
menos.
Qué – ver – des – es – tán –
tus – ár –bo – les ................(9 – 1 = 8)
Asomaba a sus ojos una lá grima ...............................(12 –
1 = 11 )
y a mi labio una frase de perdón ...............................(10 +
1 = 11)
¡Oh, terremoto mental! ..........................................(7 + 1 = 8)
Yo sentí un día en mi cráneo .....................................(9 – 1
= 8)
como el caer subitáneo ...........................................(9 -1 = 8)
de una Babel de cristal ..........................................(7 + 1 = 8)
(Ruben Darío)
FICHA PARA DESCARGAR
ACTIVIDADES INTERACTIVAS
CÓMPUTO SILÁBICO (Al terminar le vais dando a ejercicio siguiente)
CONTADOR DE VERSOS (Tenéis que pegar una poesía y luego
ya medirla)
lunes, 13 de abril de 2015
Medidas de ángulos
Para medir ángulos usamos el transportador de ángulos o semicírculo graduado.
Ponemos en el vértice el punto central inferior.
Alineamos la recta que marca cero con uno de los lados.
Y vamos contando los grados marcados en el semicírculo.
ACTIVIDADES INTERACTIVAS
MEDIMOS ÁNGULOS - ANAYA 4º
LOS ÁNGULOS Y SU MEDIDA - EL TANQUE MATEMÁTICO
MIDE LOS ÁNGULOS CON EL TRANSPORTADOR - BROMERA
MEDIDA DE ÁNGULOS
EL TRANSPORTADOR DE ÁNGULOS
FICHAS PARA DESCARGAR
Ponemos en el vértice el punto central inferior.
Alineamos la recta que marca cero con uno de los lados.
Y vamos contando los grados marcados en el semicírculo.
Clases de ángulos según su abertura:
ACTIVIDADES INTERACTIVAS
MEDIMOS ÁNGULOS - ANAYA 4º
LOS ÁNGULOS Y SU MEDIDA - EL TANQUE MATEMÁTICO
MIDE LOS ÁNGULOS CON EL TRANSPORTADOR - BROMERA
MEDIDA DE ÁNGULOS
EL TRANSPORTADOR DE ÁNGULOS
FICHAS PARA DESCARGAR
jueves, 29 de mayo de 2014
Medir la superficie de los polígonos
Para medir la superficie de las figuras planas, utilizamos el cuadrado como unidad de medida.
La superficie se mide en unidades cuadradas.
Medir una superficie es calcular el número de unidades cuadradas que tiene o que ocupa.
ACTIVIDADES INTERACTIVAS
FICHAS PARA DESCARGAR
lunes, 24 de marzo de 2014
Unidades de peso
Kilogramo
(Kg), medio kilo y cuarto de kilo
El kilogramo o kilo
(kg) es la unidad principal de medida de
peso
1 Kg = 2 medios de kilo 1 Kg = 4 cuartos
de kilo
El gramo (g) y la
tonelada (t)
Para medir pequeños pesos
utilizamos el gramo (g)
Un kilogramo tiene 1.000
gramos
1 kg
= 1.000 g
Para
medir grandes pesos utilizamos la tonelada (t)
Una
tonelada tiene 1.000 kilogramos
1
t = 1.000 Kg
ENLACES A OTRAS PÁGINAS
Suscribirse a:
Comentarios (Atom)